В 2009 г. вышел закон «Технический регламент о безопасности зданий и сооружений». В данном документе безопасность трактуется как состояние, при котором отсутствует недопустимый риск, связанный с причинением вреда жизни или здоровью граждан, имуществу физических или юридических лиц, государственному или муниципальному имуществу, окружающей среде, жизни или здоровью животных и растений. То есть в РФ нормами вводится понятие риска.
Существующая в РФ нормативная база по управлению безопасностью строительных объектов не в полной мере справляется с возложенными на нее задачами, а норм, которые регламентируют риск аварии зданий, нет вообще. Использование в строительстве методики нормирования, основанной на коэффициентах надежности, теоретически обеспечивает безопасность строительных конструкций. Однако, опыт эксплуатации конструкций показывает, что надежность является необходимым, но не достаточным условием безопасности.
Установлено, что в 80% случаев причиной строительных аварий являются грубые человеческие ошибки, допускаемые при проектировании, изготовлении и монтаже несущих конструкций, которые при невыгодном сочетании с непредсказуемыми факторами природно-климатического и техногенного характера становятся причинами обрушений строящихся и уже построенных зданий и сооружений.
Таким образом, формирование процедур и методик, позволяющих устанавливать степени конструкционной безопасности зданий с учетом риска, является весьма актуальной потребностью строительного комплекса. Механизмом практической реализации политики обеспечения безопасности строительных объектов должна стать система управления рисками на всех стадиях жизненного цикла здания и сооружения.
Технология измерения фактического риска аварии объекта
Обследование объекта не представляет интереса с точки зрения вопросов, освещаемых в работе. Необходимо отметить, что объем работ по обследованию сокращается по сравнению с общепринятыми методиками за счет снижения количества конструкций для детального обследования.
Второй этап – это формализация экспертной информации (рис.1). Для формализации может быть использовано правило, разработанное профессором А.П. Мельчаковым или математическая модель описанная в работе Л.К. Резника «Использование нечеткой информации для повышения точности измеряемых величин»:
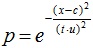 (1)
(1)
где x – фактическое числовое значение параметра дефектной конструкции;
c – проектное значение величины;
u – предельное значение величины x, соответствующее одному из предельных состояний;
t– число, равное значению, при котором р = 0,5, если x = u.
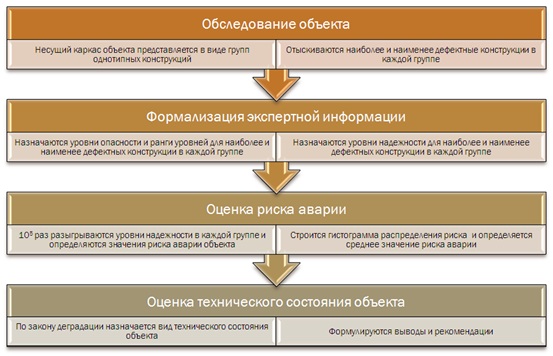
Рис. 1. Технология оценки уровня конструкционной безопасности
Для определения предельных числовых значений (u) параметров конструкции рекомендуется использовать методы и подходы, цель которых состоит в выявлении фактического запаса безопасности, заложенного в установленное проектом значение параметра. Удаление этого запаса приводит к предельному значению параметра. При этом задача формулируется следующим образом: определить числовое значение параметра, при котором действующая на конструкцию нагрузка становится предельной, соответствующей переходу конструкции в механизм.
Графики зависимости функции плотности вероятности от значения уровня надежности группы конструкций могут быть представлены, как показано на рис.2.
Для подержанных зданий разница между значениями p1 и p2 существенна. Количество более дефектных конструкций превышает количество менее дефектных. Графически закон деградации примет вид, представленный на рис.3.
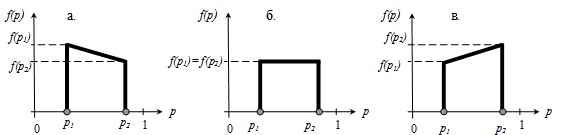
Рис. 2. Варианты вида модели закона деградации
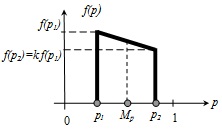
Рис. 3. Вид модели закона деградации несущих
конструкций для эксплуатируемых зданий
Площадь под законом деградации равна единице. Закон деградации группы конструкций принимает вид:
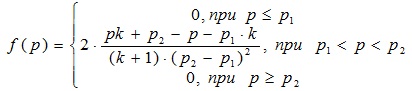 (2)
(2)
«Комплексные» показатели конструкционной безопасности здания – это закон распределения плотности вероятностей для уровней надежности конструкций в группе.
«Интегральным» показателем конструкционной безопасности здания служит закон распределения риска аварии, определенный на основе комплексных показателей, найденных для всех групп конструкций.
Построение статистического распределения фактического риска аварии основано на методе статистических испытаний (метод Монте-Карло) риск-модели (3), полученной А.П. Мельчаковым. Риск-модель связывает случайную величину риска аварии r исследуемого объекта с уровнями надежности р всех групп однотипных конструкций несущего каркаса этого объекта
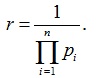 (3)
(3)
Случайные наборы представителей р от групп формируются по их «комплексным» показателям, которые являются частными случаями общего закона деградации группы после подстановки в него «единичных» показателей р1, р2и k. Каждый набор моделирует одну из возможных аварийных ситуаций объекта. В итоге, задача по построению статистического распределения риска аварии объекта сводится к разыгрыванию в каждой группе конструкций случайной величины р на основе закона ее распределения на конкретный момент времени эксплуатации исследуемого объекта. Разыгрывание случайной величины р базируется на ее связи с другой случайной величиной, для которой в компьютере имеется алгоритм для генерации. Для целей разыгрывания применяется равномерный закон распределения случайной величины q. По сути, величина q – площадь области на графике закона деградации (рис.4), ограниченной значением р1 слева и случайным значением искомой величины p справа.
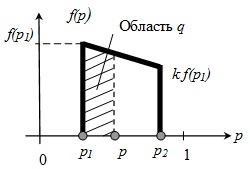
Рис. 4. Графический смысл величины q
Средний уровень надежности всех конструкций в группе (уровень надежности группыконструкций) находится в пределах от р1 до р2.
Общая формула для разыгрывания, отыскиваемая из решения определенного интеграла:
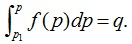 (4)
(4)
После подстановки в (4) формулы (2) и решения относительно p имеем:
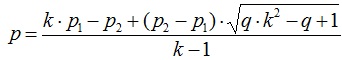 (5)
(5)
Для каждой группы однотипных конструкций в (5) подставляются минимум 105 значений q (qизменяется от 0 до 1 по равномерному закону) и соответствующие группе конструкций значения «единичных» показателей р1, р2 и k. В результате для каждой группы однотипных конструкций получаем 105 значений р. Затем, воспользовавшись формулой (3), получаем 105 значений r. Статистический ряд случайной величины риска аварии rпозволяет построить для исследуемого строительного объекта на текущий момент времени его эксплуатации гистограмму распределения риска (рис.5). По гистограмме несложно определить статистические характеристики риска аварии: среднее значение риска аварии; стандартное значение риска; вероятность безаварийной работы и т.д.
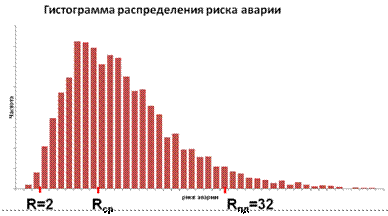
Рис. 5. Гистограмма распределения риска аварии
Закон распределения плотности вероятности риска аварии объекта в процессе эксплуатации размывается (деградирует) (рис.6). При этом степень неопределенности технического состояния несущего каркаса объекта, показателем которой является величина информационной энтропии, увеличивается.
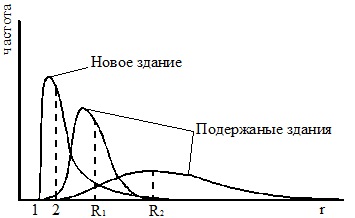
Рис. 6. Закон распределения плотности вероятности риска аварии
объекта в процессе эксплуатации размывается
Получен закон деградации несущего каркаса строительного объекта в координатах «риск аварии-энтропия». Анализ этих работ позволяет сделать следующие выводы по рассматриваемой задаче:
1. Существуют пороговые значения риска аварии, при достижении которых строительный объект переходит в качественно иное состояние – из безопасного в аварийное, а из аварийного состояния в ветхо-аварийное. Эти значения равны 15 и 83 соответственно.
2. Пороговые риски аварии не зависят ни от конструктивного типа здания (сооружения), ни от его этажности. Они являются инвариантами, что вытекает из способа доказательства их существования.
Показатель «энтропия» является сложным для вычисления и практического применения. Вместе с тем, существует физический аналог понятия «энтропия» – конструкционный износ объекта, который, как и энтропия, характеризует степень деградации несущего каркаса. Поэтому целесообразно закон деградации строительного объекта отыскивать в виде диаграммы, показывающей взаимосвязь конструкционного износа несущего каркаса объекта и величины его среднего риска аварии.
Для построения математической модели оценки конструкционного износа здания вводятся две гипотезы. Первая из них утверждает, что формой модели роста износа объекта в процессе его эксплуатации является экспонента, а ее представительным параметром служит величина среднего риска аварии объекта R. Вторая гипотеза предполагает, что в момент перехода объекта в ветхо-аварийное состояние ресурс его несущего каркаса по износу составляет 5%. Принятым гипотезам отвечает следующая математическая модель:
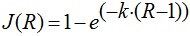 , (6)
, (6)
где J(R) – физический износ;
k – коэффициент, полученный в работах А.П. Мельчакова, равен 0,0365;
R – риск аварии.
Целесообразно интервал между пороговыми значениями риска аварии разделить на два участка; в одном из них состояние объекта обозначить как предаварийное, а в другом как аварийное. Критическим значением риска аварии объекта следует признать значение, равное 32. Это значение риска – среднее, для зданий различного уровня ответственности данное значение может колебаться. Но для зданий и сооружений нормального уровня ответственности риск, равный 32, как и пороговые значения риска аварии, следует признать инвариантом, то есть не зависящим от конструктивного типа объекта и его этажности.
В окончательном виде модель деградации показана на рис.7. На рис.7 можно четко определить три зоны:
1. Эксплуатация объекта с момента окончания его строительства до достижения риском аварии точки А – безопасное состояние. Объект способен сопротивляться многим не учтенным при проектировании нагрузкам.
2. Эксплуатации объекта с момента окончания его строительства до достижения риском аварии точки В определяет безопасный ресурс объекта. Техническое состояние объекта – предаварийное, а величину риска аварии, равную 32, следует принять за критический риск аварии.
3. Риску, равному 32, соответствует износ 68%. При такой величине износа требуется капитальный ремонт здания. Техническое состояние объекта – аварийное. К моменту достижения значения риска аварии, равного 83, способность несущего каркаса объекта сопротивляться любым нагрузкам теоретически исчерпывается.
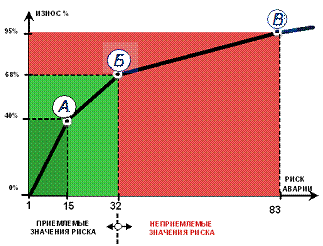
Рис. 7. Модель деградации несущего каркаса объекта
Модель деградации позволяет не только произвести оценку по величине риска аварии вида технического состояния здания (сооружения) на любой стадии его жизненного цикла, но и сформировать стандарт на величину риска аварии строительного объекта.
При известном значении риска аварии можно определить величину безопасного остаточного ресурса:
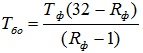 , (7)
, (7)
где Тбо – безопасный остаточный ресурс;
Тф – фактическое время эксплуатации объекта;
Rф – риск аварии;
На величину безопасного ресурса влияние оказывает не только величина риска аварии на момент окончания строительства объекта, но и время его возведения. Использование формулы, приведенной выше, и приемов нечеткой логики позволяет сделать вывод о том, что наибольший безопасный ресурс достигается в случае, если срок возведения объекта и величина риска аварии к моменту окончания строительства нормативные.
Выводы
Выполненные исследования по решению задачи оценки и регулирования риска аварий эксплуатируемых зданий показали:
1. Предложенная технология прогнозирования конструкционной безопасности существующих зданий и сооружений может быть использована на практике для оценки риска аварии и вида технического состояния. Она одобрена и рекомендована к применению Управлением государственного строительного надзора Министерства строительства, инфраструктуры и дорожного хозяйства Челябинской области и Рабочей группой по предупреждению аварий зданий и сооружений с массовым пребыванием людей при КЧС Челябинской обл.
2. Предложенная модель закона деградации строительного объекта обеспечивает определение вида технического состояния эксплуатируемых зданий и сооружений.
3. В пределах интервала риска аварии 15-83 техническое состояние объекта считается аварийным, но в зависимости от величины риска аварии имеет различную степень опасности. Целесообразно интервал между пороговыми значениями риска аварии разделить на два участка: предаварийное и аварийное состояние. Точкой, разделяющей этот интервал, является точка, соответствующая риску 32. Данное значение справедливо для зданий нормального уровня ответственности.
4. Так как при оценке технического состояния зданий и сооружений нет необходимости в детальном обследовании всех конструкций, предложенная технология прогнозирования конструкционной безопасности является менее трудоемкой. Это, в том числе, позволяет ввести в практику страховой и сертификационный механизмы, которые являются экономически эффективными способами регулирования безопасности объектов строительства.