РЕАЛИЗАЦИЯ НЕЛИНЕЙНОЙ ДЕФОРМАЦИОННОЙ МОДЕЛИ ПРИ РАСЧЕТЕ ПРОЧНОСТИ ТРУБОБЕТОННЫХ КОЛОНН

Трубобетонные колонны (ТБК) очень эффективно используются в качестве сильно нагруженных несущих элементов и обеспечивают высокую безопасность зданий и сооружений [3]. Широкое применение трубобетонных колонн (ТБК) в нашей стране сдерживается отсутствием отечественных норм по их проектированию и расчету. Несмотря на весьма обстоятельные исследования в этой области, надо признать, что до сих пор нет надежной и приемлемой для практического использования расчетной модели трубобетонного сечения в предельном состоянии, адекватно отражающей его специфические особенности. Это и неудивительно, принимая во внимание серьезные и многочисленные трудности, обусловленные сложностью самой системы “бетонное ядро-стальная оболочка”, работающей в условиях объемного сжатия (рис.1), и сложностью описания процессов перераспределения усилий между компонентами системы в этих условиях. По этой причине до сих пор актуален вопрос об установлении четкого критерия, соответствующего наступлению первого предельного состояния ТБК. В этой связи можно полагать, что дальнейшие исследования в этой области необходимы, полезны и перспективны.

Анализ данных многочисленных экспериментальных исследований позволил принять следующий критерий предельного состояния центрально сжатого трубобетонного элемента.  Предельное состояние наступает при выполнении следующих условий:

• достижение нормальными напряжениями осевого направления в бетоне ядра  значения прочности бетона при трехосном сжатии σ_bz = R_b3;
• достижение интенсивности напряжений в наиболее сжатом  волокне стальной оболочки физического или условного предела текучести σ_pi = σ_p,y;
• достижение нормальными напряжениями осевого направления в наиболее растянутом волокне стальной оболочки предела текучести σ_pz = σ_p,y.

Учитывая внутреннюю статическую неопределимость трубобетонной конструкции первое условие наступления предельного состояния должно выполняться совместно со вторым или третьим.

а)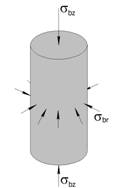

б)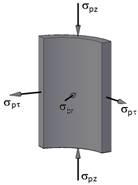

Рис. 1. Напряженное состояние бетонного ядра (а)
и стальной оболочки (б) при осевом сжатии ТБК

C целью обеспечения эксплуатационной пригодности ТБК при действии на нее расчетных нагрузок величины деформаций стальной оболочки (в наиболее сжатом волокне – интенсивность деформаций ε_pi, в наиболее растянутом волокне – осевая деформация ε_pz),совместно с осевыми деформациями бетонного ядра ε_bz, должны ограничиваться соответствующими значениями.

В связи с этим расчет прочности нормальных сечений ТБК в общем случае внецентренного сжатия следует производить на основе нелинейной деформационной модели железобетона с учетом особенностей деформирования бетонного ядра и стальной оболочки в условиях объемного напряженного состояния. Для более точного расчета также следует учитывать неупругие деформации материалов и изменение коэффициентов поперечных деформаций в бетонном ядре и стальной оболочке по мере роста уровня напряжений.

Переход от эпюры напряжений в бетоне и стальной обойме к обобщенным внутренним усилиям производят с использованием процедуры численного интегрирования напряжений по нормальному сечению. Для этого нормальное сечение условно разбивают на малые участки (рис.2) с площадями бетона A_bi и стальной оболочки A_pk, в пределах которых напряжения принимают равномерно распределенными (усредненными).

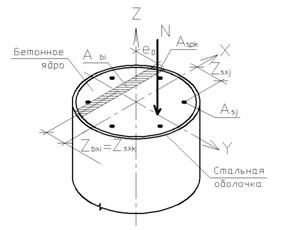
Рис. 2. Схема к расчету прочности трубобетонного элемента

Общую систему физических соотношений для расчета  нормальных сечений ТБК по прочности, как и в традиционной деформационной модели [8], получают из совместного рассмотрения:

• уравнений равновесия внешних сил и внутренних усилий в нормальном сечении элемента;
• уравнений, устанавливающих распределение осевых деформаций в бетоне и арматуре по нормальному сечению, исходя из условия плоского поворота и плоского смещения сечения;
• зависимостей, связывающих напряжения и относительные продольные деформации бетона, стальной обоймы и продольной арматуры.

Основной особенностью расчета сжатых трубобетонных элементов является отсутствие исходных диаграмм для бетона и металла, работающих в условиях неоднородного напряженного состояния. В связи с этим расчет нормальных сечений  ТБК по прочности  выполняют в два этапа. На первом этапе расчетным путем определяют зависимости между напряжениями и деформациями осевого направления в бетонном ядре и стальной оболочке «σ_bz— ε_bz» и «σ_pz— ε_pz» при кратковременном действии на трубобетонный элемент осевой сжимающей нагрузки. В рассматриваемой конструкции бетонное ядро и стальная оболочка работают в условиях неоднородного напряженного состояния, поэтому вопросам установления указанных аналитических зависимостей  следует уделить особое внимание.

В центрально сжатых трубобетонных элементах, имеющих круглую или кольцевую форму поперечного сечения, через каждую точку тела перпендикулярно продольной оси условно можно провести плоскость изотропии. В этой связи можно использовать основные уравнения и допущения трансверсально-изотропной модели бетона, принятой в работе [4].
Система уравнений, описывающих связь между напряжениями и деформациями в осевом (индекс «z») и радиальном (индекс «r») для любой точки трансверсально-изотропного бетонного ядра в упругой и упруго-пластической стадиях, имеет следующий вид:

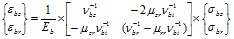,                   ( 1)

где E_b – начальный модуль упругости бетона.

Учет неупругих свойств объемно сжатого бетонного ядра производится путем использования в расчете прочности переменных коэффициентов упругости ν_bj(j=z,r,i) и поперечной деформации μ_zr,μ_rr бетона.

Текущие значения коэффициентов поперечной деформации бетона продольного и радиального направлений μ_jr(j = z,r), находятся по известной [5] формуле

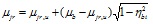,                                      (2)

где η_bi – уровень интенсивности напряжений в бетонном ядре;

μ_b = 0,18÷0,25 – коэффициент Пуассона для бетона (при отсутствии точных данных рекомендуется принимать μ_b = 0,2;

μ_jr,u– предельное значение коэффициента поперечной деформации μ_jr для бетона,

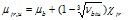.                                           (3)

Значение параметра χ_jr, предложенного Н.И.Карпенко для учета того обстоятельства, что в состоянии неравномерного трехосного сжатия коэффициенты μ_jrпо главным направлениям могут существенно различаться, применительно к ТБК вычисляется по формуле

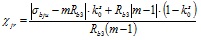,                        (4)

где   s = -1 – для тяжелого бетона;

s = -2 – для мелкозернистого бетона;

k₀ – коэффициент, определяемый по формуле (19).

Для вычисления коэффициента упругости бетона можно принимать любые известные зависимости, обеспечивающие достаточную точность оценки напряженно-деформированного состояния конструкции, например предложенную в работе 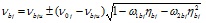[5]:

,                      (5)

где η_bj – уровень напряжений в бетонном ядре по направлению j;

ν_0j, ν_bju – значения коэффициента упругости в базовых точках диаграммы;

ω_1bj, ω_2bj,– коэффициенты, характеризующие кривизну соответствующей диаграммы, причем

ω_2bj = 1 — ω_1bj                                                 (6)

При расчете ТБК круглого сечения параметры зависимости (5) для вычисления коэффициента упругости бетона определяют с учетом неоднородного напряженного состояния бетона и сложного режима загружения по формулам:

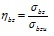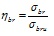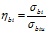;                  ;                ;                 (7)

• для восходящей ветви диаграммы в формуле (3) принимают знак «+» и

ν_0j=1;                     ω_1bj=2-2,05ν_bju;                            (8)

• для нисходящей ветви диаграммы в формуле (5) принимают знак «-» и

ν_0j=2,05ν_bju;              ω_1bj=1,95ν_bju-0,138;               (9)

где  ν_bju  – значения ν_bj в вершинах соответствующих диаграмм «σ_bj— ε_bj», определяемые из выражения

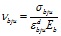.                                                               (10)

Для определения напряжений в вершинах диаграмм «σ_bj— ε^d_bj» предлагаются следующие формулы:

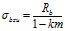;                                                             (11)

σ_bru= mσ_bzu,                                                             (12)

где m   – уровень бокового обжатия бетона в предельном состоянии;

k – коэффициент бокового давления.

Установлено, что применительно к ТБК значение k зависит от конструктивного коэффициента трубобетона ρ и может быть вычислено по формуле

k=7-1,2ρ,                                                                 (13)

в которой
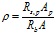,                                                                     (14)

где   A, R_b, A_p, R_s,p – площади поперечного сечения и расчетные сопротивления бетонного ядра и стальной оболочки.

Для определения уровня бокового обжатия m предлагается следующая формула

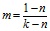 ,                                                               (15)

в которой n=b(k-0,5) при значении коэффициента b=0,096 (для тяжелого бетона).

Для осевого и трансверсального направлений величины коэффициентов упругости ν_bju, определяющих значения диагональных деформаций (деформации главной диагонали, вычисленные без учета влияния коэффицинтов поперечной деформации), находятся в зависимости от напряжений σ_bzu,σ_bru и предельных деформаций ε^d_bzu , ε^d_bru.

Данные деформации находят в зависимости от полных относительных деформаций ε_bzu и ε_bru, соответствующих выходу напряжений на поверхность прочности и связанных с диагональными следующими зависимостями, вытекающими из системы (1):

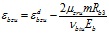;                                                       (16)

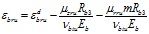.                                             (17)

Предельные полные деформации осевого направления ε_bzu   рекомендуется вычислять по формуле

ε_bzu = k₀ε_b0,                                                             (18)

где   ε_b0 – величина относительной деформации бетона в вершине диаграммы «σ_b—ε_b» при осевом сжатии и однородном напряженном состоянии бетона, принимаемая равной 0,002 при непродолжительном действии нагрузки и по СП 52-101-2004 – при продолжительном действии нагрузки;

k₀ — коэффициент, учитывающий неоднородное напряженное состояние бетонного ядра ТБК.

Коэффициент k₀ для условий трехосного сжатия σ₁=σ₂>σ₃ и простого режима нагружения (при сохранении постоянного соотношения между напряжениями) можно вычислять согласно рекомендациям европейских норм [1]. В ТБК реализуется сложный режим загружения, характеризующийся не пропорциональным ростом напряжений σ₁,σ₂,σ₃. В процессе увеличения внешней сжимающей нагрузки постоянно растут по модулю осевые напряжения σ₃=σ_bz. Напряжения трансверсального направления в квазиупругой стадии работы близки к нулю или даже могут иметь незначительное растяжение. С образованием микротрещин в бетоне они меняют знак и в предельном состоянии достигают максимальной сжимающей величины – σ_bru.

Такой режим нагружения приводит к снижению значения относительной деформации ε_bzu в вершине диаграммы «σ_bz—ε_bz» по сравнению с простым режимом. Для учета данного обстоятельства с помощью компьютерной программы «Microsoft Excel» были обработаны результаты экспериментов 75 опытных образцов ТБК и получена следующая формула

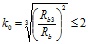.                                                            (19)

Ограничение k₀ ≤ 2 рекомендуется вводить для исключения чрезмерных деформаций трубобетонных колонн.

Значения коэффициентов упругости ν_bi и поперечных деформаций μ_zr в матрице податливости системы (1) определяют величину деформаций вдоль одного (осевого или трансверсального) направления, обусловленных напряжениями другого направления (соответственно трансверсального или осевого). Для их определения рекомендуется использовать величины интенсивности напряженийσ_bi и интенсивности деформаций ε_bi.

Из положений механики твердого тела [7] известно, что интенсивность напряжений является вполне определенной независящей от вида напряженного состояния функцией интенсивности деформаций σ_i=F(ε_i). Поскольку функция F(ε_i) зависит только от материала, то любой вид объемного напряженного состояния в области упругих, упругопластических и пластических деформаций можно свести к простейшим видам напряжения, построив соответствующую кривую σ_i=F(ε_i).

Для бетона воспользуемся рекомендуемой нормами зависимостью «σ_b—ε_b» при одноосном сжатии. Соответствующая зависимость между интенсивностями напряжений и деформаций может быть записана в таком же виде

σ_bi = ν_biE_bε_bi.                                                          (20)

Запишем выражения для определения σ_bi и ε_bi применительно к ТБК, имеющим круглое сечение

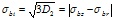;                                                (21)

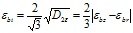,                                           (22)

где D₂ и D_2ε – вторые инварианты девиаторов напряжений и деформаций.

Подставив в уравнение (20) выражения для определения σ_bi  и ε_bi, получим формулу для вычисления относительной радиальной деформации в предельном состоянии бетонного ядра ε_bru
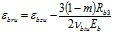.                                                      (23)

В формулах (16), (17) и (23) предельное значение коэффициента упругости ν_biu в первом приближении может быть принято равным ν_bzu. В ходе дальнейших расчетов это значение уточняется.

При расчете ТБК по нелинейной деформационной модели в качестве расчетных диаграмм состояния стальной оболочки и продольной стержневой арматуры рекомендуется принимать криволинейные диаграммы. Допускается  в качестве расчетных диаграмм состояния стальной оболочки и продольной стержневой арматуры принимать двухлинейную диаграмму в соответствии  указаниями СП 52-102-2004. Диаграммы состояния стали при растяжении и сжатии принимают одинаковыми.

В сжатой зоне ТБК стальная оболочка работает в условиях сложного напряженного состояния. Чтобы построить для нее  расчетную диаграмму состояния воспользуемся известной гипотезой единой кривой, предложенной А.А.Ильюшиным [2]. Согласно этой гипотезе, зависимость между напряжениями и деформациями «σ_s,p—ε_s,p», полученную при одноосном растяжении, можно считать действительной для всех напряженных состояний при замене текущих напряжений σ_s,p и текущих деформаций ε_s,p на интенсивность текущих напряжений ε_s,pi и интенсивность текущих деформацийes,pi соответственно.

В нашем случае мы рассматриваем напряжения и деформации, возникающие по главным площадкам, т. е. касательные напряжения и сдвиговые деформации здесь равны нулю. Тогда выражения для определения интенсивности напряжений и деформаций записываются в следующем виде:

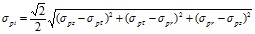;             (24)

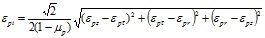.           (25)

Связь между деформациями и напряжениями для любой точки внешней стальной оболочки в упругой и упруго-пластической стадиях описывается системой уравнений:

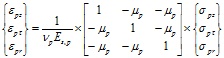.                     (26)

где σ_pz, σ_pτ, σ_pr – нормальные (главные) напряжения в трубе в продольном, тангенциальном и радиальном направлениях;

ε_pz, ε_pτ, ε_pr – относительные деформации стальной оболочки по соответствующим направлениям;

E_s,p – начальный модуль упругости стали;

ν_p– коэффициенты упругости стали;

μ_p– коэффициент поперечной деформации стали трубы.

При наличии в бетонном ядре стержневой арматуры связь между  нормальными напряжениями в ней σ_s и относительными деформации ε_sописывается известной зависимостью

σ_s =E_sε_sν_s ,                                                               (27)

где ν_s  – коэффициент  упругости арматуры.

При криволинейной диаграмме для вычисления коэффициентов упругости стальной оболочкиν_p и арматуры ν_s можно принимать любые известные зависимости, аналогичным принятым для бетона [6].

Для вычисления коэффициента поперечной деформации стальной оболочки μ_p предлагается следующая формула

μ_p = 0,5 — (0,5-μ₀)(ν_p —ν_pu )/(1-ν_pu ) ,                      (28)

где ν_pu   – значение коэффициента упругости, соответствующее расчетному значению сопротивления стали;

μ₀ – коэффициент Пуассона для стали.

В результате каждому значению относительных деформаций осевого направления ε_bi, ε_pk и ε_s, которые в процессе расчета постепенно увеличивают с заданным шагом, устанавливают соответствующие величины напряжений σ_bi, σ_pk и σ_s. Только после этого переходят ко второму этапу расчета, суть которого изложена выше.

Таким образом, получена методика построения аналитических зависимостей, устанавливающих связь между напряжениями и деформациями осевого направления в бетонном ядре и стальной оболочке. Это позволяет реализовать нелинейную деформационную модель железобетона при определении прочности внецентренно сжатых ТБК.

Автор публикации

0

не в сети 8 лет

Kacenelenbaum

Комментарии: 0Публикации: 10Регистрация: 11-02-2016